Accueilretour
précédentsuivant

La notation polonaise inverse (RPN)

La genèse

Les ancêtres

Séries Classic - Woodstock

Série Spice

Série Coconut

Série Voyager

Série Pioneer

Modèles divers

Perspectives

Les manuels

La notation RPN

  Logique RPN

    Touche ENTER↑

  Pile opérationnelle

    Duplication de "T"
    LASTx
    Manipulations

  Exemples

La programmation

Liens

 Les machines HP ne sont ni les seules, ni les premières [1] à utiliser la fameuse notation polonaise inverse (RPN = Reverse Polish Notation). Mais elle reste indissociable de la marque, qui l'a généralisée et développée jusqu'à la perfection.

Le manuel complémentaire "La solution de vos problèmes avec votre calculateur Hewlett-Packard" commence par cette profession de foi :

"ENTER ↑
Cette touche est la clef de la résolution aisée et sûre de vos problèmes. Elle est à la base de la logique polonaise inverse de votre calculateur Hewlett-Packard. Logique si simple, si puissante que, l'ayant utilisée une fois, vous ne saurez plus vous contenter d'une autre."

Essayez ! Si vous n'avez pas de calculateur RPN HP sous la main (condoléances...), vous pouvez quand même tester les manipulations proposées ci-dessous. Rendez-vous sur la page de liens, rubrique "Émulateurs"...

La logique RPN

La notation polonaise a été inventée en 1920 par le mathématicien Jan Łukasiewicz. Il recherchait un système de codage des expression mathématiques dépourvu de parenthèses, mais néanmoins capable de traiter toute formule sans ambiguïté. Dans cette notation, les opérateurs précédaient les arguments [2] :

2 × (3 + 4)

était codé

× 2 + 3 4

Vers la fin des années 50, avec l'apparition des ordinateurs, Charles L. Hamblin s'intéresse à la version postfixée de cette notation. Elle est en effet particulièrement bien adaptée à la manière dont les processeurs traitent leurs opérandes. Dans cette notation, ceux-ci sont introduits en premier, et notre exemple ci-dessus devient

3 4 + 2 ×

En 1972, à l'apparition du HP-35, Hewlett-Packard adopte la dénomination "notation polonaise inverse" en l'honneur de Łukasiewicz.

La touche ENTER↑

Évidemment, il faut séparer le premier nombre introduit du deuxième. Sinon, dans l'exemple précédent, comment distinguer la succession des deux opérandes 3 et 4 du nombre à deux chiffres 34 ?

C'est le rôle de la touche ENTER↑. Notre exemple s'écrirait donc sur une machine HP :

3  ENTER↑ 4 + 2 ×

Faisons deux remarques :
  • après avoir effectué 3  ENTER↑ 4 +, dont le résultat s'affiche immédiatement, il n'est pas nécessaire de rappuyer sur ENTER↑. En effet, la machine "sait" qu'il s'agit d'un calcul antérieur, et non du début d'un nombre introduit par l'utilisateur. Il en est de même pour toute fonction d'une ou deux variables : son application sépare automatiquement son résultat de l'entrée suivante, évitant de retaper ENTER↑.
  • même dans un exemple aussi simple, la notation RPN est plus économe en frappes de touches que le calcul algébrique, qui s'écrirait 2 × (3 + 4) =. Ce dernier exige 8 frappes au lieu de 6. Ce n'est qu'un début.

    haut de page

La pile opérationnelle

Il ne s'agit pas seulement de séparer les nombres. Après avoir tapé "3  ENTER↑ 4", le 4 apparaît à l'affichage. Où est passé le 3 ? Il est bien en réserve quelque part. La pile opérationnelle RPN HP "empile" les arguments selon le principe LIFO (Last In, First Out) : le premier à "sortir" est le dernier entré.

Notre 3 est donc dans le 2ème "étage" de la pile, dénommé Y (le premier niveau, X, étant celui qui est affiché). La pile opérationnelle HP comporte 4 [3] niveaux : X, Y, Z et T. Observons son comportement dans l'exemple précédent :

frappe :
 3
 ENTER↑ 4
 +
 2
 ×
T





Z





Y
3
 3
7
(affichage) X
 3
 3
 4
 7
 2
 14

Remarquons ce qui se passe à l'endroit du 3 : après avoir tapé ENTER↑, la pile est "verrouillée" et le 4 "écrase" le 3. Dans pratiquement tous les autres cas [4], le nombre nouvellement introduit "pousse" les autres d'un étage. (Si un nombre était présent dans le registre T, il est perdu [5].)

Le calcul précédent aurait également pu être réalisé sous la forme 2×(3+4). En RPN on aurait noté

2 ENTER↑ 3  ENTER↑ 4 + ×

... et la pile se serait comportée ainsi :

frappe :
 2
 ENTER↑ 3
 ENTER↑
 4
 + ×
T






Z


2
 2

Y
2
 2
 3
 3
 2
(affichage) X
 2
 2
 3
 3
 4
 7
 14

On note que cette seconde possibilité nécessite une pression de touche de plus. Elle utilise aussi un niveau de pile supplémentaire (Z). Il y a encore de la marge (avec T), mais on conçoit que les expression les plus complexes nécessitent un minimum de discernement pour ne pas faire "déborder" la pile. Typiquement, elles doivent être calculées "par l'intérieur", en commençant par les sous-expressions les plus internes. Comme les modes d'emploi HP l'illustrent fort bien, c'est l'ordre qui serait employé dans le cas d'un calcul "manuel".

Duplication de "T"

Comme on le voit dans les deux exemples ci-dessus, une opération (+, ×...) combine les contenus de X et Y et place le résultat dans X. Cela fait "redescendre" Z dans Y et T dans Z. Mais HP a prévu une caractéristique judicieuse du registre T :

Lorsque la pile redescend, le contenu de T reste inchangé.

Dans ce cas, l'ancien "T" se retrouve donc dans Z et dans T : il est "dupliqué". Cette caractéristique anodine a des applications pratiques. Les exemples suivants sont adaptés du manuel du HP-15C :

Progressions géométriques

"Un bactériologiste étudie un certain micro-organisme dont la population croît de 15% par jour (facteur de croissance égal à 1,15). S'il commence avec un échantillon de 1000 quelle sera la population à la fin de chaque journée pendant les 4 premier jours ?"


 1.15
 ENTER↑ ENTER↑ ENTER↑
 1000
 × × × ×
T


1,15 1,15 1,15 1,15 1,15 1,15
Z

1,15 1,15 1,15 1,15 1,15 1,15 1,15
Y
1,15 1,15 1,15 1,15 1,15 1,15 1,15 1,15
X
 1,15
 1,15 1,15 1,15 1.000
 1.150
 1.322,50
 1.520,8750
 1749,0063

Calculs avec constante

"Parmi les étoiles les plus proches de la Terre, Rigel Kentaurus et Sirius se situent respectivement à 4,3 et 8,7 années-lumière. Utilisez la vitesse de la lumière (3×108 m/s ou 9,5×1015 m/an) pour calculer leurs éloignements en mètres."


 9.5
 EEX 15 ENTER↑
 ENTER↑ ENTER↑ 4,3 × CLx
 8,7
 ×
T




9,5   15 9,5   15 9,5   15 9,5   15 9,5   15 9,5   15
Z



9,5   15 9,5   15 9,5   15 9,5   15 9,5   15 9,5   15 9,5   15
Y


9,5   15 9,5   15 9,5   15 9,5   15 9,5   15 9,5   15 9,5   15 9,5   15
X
 9,5
 9,5   00 9,5   15 9,5   15 9,5   15 9,5   15 4,3
 4,1   16
 0,0 8,7
 8,3   16

Ce dernier exemple tire parti d'une caractéristique de la touche d'effacement (CLx). On le voit colonne 9 (0,0), celle-ci, à l'instar de ENTER↑, verrouille la pile (cf. [4]), de sorte que le multiplicateur constant dans Y, Z et T reste inchangé.

En fait, l'exemple original du manuel du HP-15C n'utilisait pas la duplication de T, mais le registre LASTx.

Registre LASTx

Le registre LASTx mémorise la dernière valeur du registre X de la pile avant l'exécution d'une fonction, qu'elle soit d'une ou de deux variables.

Cela offre une autre possibilité pour les calculs avec constante : voici comment l'exemple précédent était présenté dans le manuel du HP-15C :


 4.3
 ENTER↑ 9.5 EEX
 15 × 8,7
 LASTx
 ×
T








Z






4,1   16
Y
4,3
 4,3
 4,3 4,3
4,1   16 8,7 4,1   16
X
 4.3
 4,3 9,5 9,5   00 9,5   15 4,1   16
 8,7 9,5   15
 8,3   16

LASTx




9,5   15
 9,5   15 9,5   15 9,5   15

Cette fois la constante est introduite en dernier, et reste dans le registre LASTx.

Mais ce registre supplémentaire a aussi un autre emploi évident : la correction d'erreurs. Pour annuler une opération appliquée à un argument incorrect, il suffit de rappeler LASTx et d'effectuer la fonction inverse. Par exemple :

frappe :
 affichage :
287
 287
ENTER↑
 287,0000
12.9
 12,9
÷
22,2481

Oops ! 12.9 était faux, c'était 13.9 qu'il fallait écrire :

frappe :
 affichage :
LASTx
 12,9000
× 287,0000
13.9
 13,9
÷
20,6475

On a simplement rappelé LASTx puis effectué la fonction inverse (×) pour revenir à l'état antérieur.

Manipulations de la pile

La pile RPN ne se contente pas de mémoriser statiquement les résultats intermédiaires. Elle peut être réordonnée à volonté grâce aux opérations de manipulation suivantes :

Touche x⇄y

Cette touche effectue un échange (transposition) des registres X et Y. Elle est bien utile pour remettre les arguments dans l'ordre avant une opération non commutative (− ou ÷). Son effet se décrit ainsi, en supposant que la pile contienne les nombres 1, 2, 3 et 4 :


 x⇄y
T
 1
 1
Z
 2
 2
Y
 3
 4
X
 4
 3

Touche R↓

Cette touche "Rotate down" permet "d'aller chercher" tout nombre contenu dans la pile, ou simplement d'en vérifier le contenu. Elle fait défiler celle-ci de bas en haut (permutation circulaire) :


 R↓
T
 1
 4
Z
 2
 1
Y
 3
 2
X
 4
 3

Bien sûr, au bout de 4 appuis sur la touche R↓, la pile est rétablie dans son état initial. Cependant, pour plus de souplesse, plusieurs calculateurs HP proposent la fonction R↑, qui effectue la permutation inverse. Elle est généralement située en fonction secondaire de R↓.

Les touches x⇄y et R↓ permettent d'effectuer toute permutation [6] des 4 niveaux de la pile. On peut donc se passer, dans pratiquement tous les calculs manuels, de la mise en mémoire des résultats intermédiaires.

haut de page

Exemples

L'exemple suivant est récurrent dans les modes d'emploi HP (ici, le HP-15C). Il s'agit de calculer l'expression :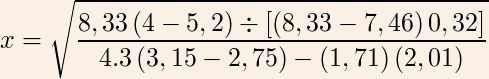

Une solution possible est donnée dans les manuels. Elle tire parti de LASTx pour éviter d'introduire deux fois 8,33 :

4 ENTER↑ 5.2 − 8,33 × LASTx 7,46 − 0,32 × ÷ 3,15 ENTER↑ 2,75 − 4,3 × 1,71 ENTER↑ 2,01 × − ÷ √

Comparez avec votre calculatrice -- si ce n'est pas une HP...

Méthode de Horner

La méthode de Horner consiste à réécrire un polynôme pour le calculer avec uniquement des multiplications. Elle évite tout recours à la fonction puissance. Par exemple (selon le manuel du HP-41CX) :

x4 − 2x3 + 5x

 = 

(x3 − 2x2 + 5)x


=

((x2 − 2x)x + 5)x


=

(((x − 2)x)x + 5)x

Ce principe s'adapte remarquablement à la pile RPN. On la remplit avec la valeur x en laquelle on souhaite calculer le polynôme. Ensuite, la duplication de T fait le reste, et évite toute mise en mémoire ou appel à la fonction puissance.

Calculons le polynôme précédent en x = 3. On commence à remplir la pile de 3 (3 ENTER↑ENTER↑ENTER↑). On continue ainsi :


 [...]
 2 − × ×
 5 + ×
T
 3
 3
 3
 3
 3
 3
 3
 3
Z
 3
 3
 3
 3
 3
 3
 3
 3
Y
 3
 3
 3
 3
 3
 9
 3
 3
X
 3
 2
 1
 3
 9
 5
 14
 42

La généralisation est immédiate, quel que soit le degré du polynôme.

haut de page

Notes

[1]  En 1963, la Friden EC-130 précède le HP-9100 de 5 ans ! Il est vrai qu'elle n'est pas programmable.

[2]  On parle de notation préfixée.

[3]  3 seulement sur le HP-9100.

[4]  On parle de fonction autorisant -- cas général -- ou interdisant les mouvements de la pile. Ce dernier cas, exceptionnel, ne concerne que les fonctions ENTER↑, CLx (effacement), Σ+ et Σ− (mise en mémoire et effacement des données statistiques). Ce comportement est resté remarquablement cohérent à travers les différentes générations de calculateurs HP.

[5]  Si la valeur présente dans T avait encore de l'importance, cette situation dénoterait assurément une mauvaise utilisation de la pile RPN.

[6]  Matheux, réveillez-vous ! Une transposition et un cycle d'ordre n engendrent le groupe symétrique 𝔖n entier !

haut de page