Accueilretour

Systèmes historiques

4. substitutions polyalphabétiques (2)

Généralités

Stéganographie

Cryptanalyse

Littérature

Transpositions

Subs. monoα

Subs. polyα 1 - 2

le chiffré

longueur de clef

1ère lettre

lettres suivantes

décryptage

conclusion

One-time pad

DES 1 - 2

Clef publique

Knapsack

Diffie-Hellman

RSA 1 - 2

Grands noms

Références



 Nous effectuons ici la cryptanalyse d'un message chiffré selon le système Vigenère.

Le chiffré

BSEVGGGXREMBACDNFCTZQUEZZQUGMICIRLBBIVYW
BMNFAWLFNZVCTSOCIKMCBLLMVCZKFNWJMGZIRZZL
ZGRIEAOHFLLRQVLHYVFXJLHNMIZKASBSEVCPHMIC
VYCVTVBVLODXFCTKSUETQVLODTIMOPSAXFCTXIRP
QVSSASZAGTWCEIQTLODWVKQURCSLZTPOWXKWWQCD
JQNSIRJZBFPFNGIWKZHDHFVEYSWZVZULFVEMQNSS
ZVKFBJNRKINHHASZAKLANJFQUSOAGYMCSZJMKMPH
JRKXWPGUIJBTVAYIKBGZDDMJBQBHNPRZOLSNRDIT
VNIKTGZDNXZBULBOEEBUCSWEZMPAQAETPGYGDVCI
JVNIKAQBTOPRVVKOWWCMWYHASDXGPARXRQGUHUIT
CPFXRRCSBOCVZMOLHXYIJTHJJRKTGZTRPJLCHFXR
VVYSUIJDKLIGGIMPLODBKWWAPAYEQUWOAPRZQBWU
VTGZTNQDMUZOBWVGCPSWXVVHPZJRKTGBFZYVVQBW
PVMVZSVSHCCPSWXAMVHBCHVARPSAVVACBLQISZGB
JPRKKUEDMVUGMCRWJCTJSBQLZUASWISZGBLJZVCI
SBIKJQPHNYODKUFNRKMVSSDVJPWLSBVRQNSORIEB
LBXMIKNHWASEAQUBJRKAQBGUIJVWLSBECIUPLRID
HVWBWLZUHHXYILGNFJRZBUPVJYKMSBODWFUOLHUE
ONLTJMJIKAGXREQFZWMYIMSBSUITTCPFUILBGUJJ
ENQBRASPMGSSASZZGCWWXIQCUHJKFZILRNTCWALS
XTZKHQNWYMDYSDBJWPAPXRJUWZWLMVVUHICSLZFB
XMAWALIGVZIKLBCXFCUSSBEEKKLBBULQNLGXMIAQ
HJWJQUHICIDXNLSCHVTKISAIEBCSOBIGBKLANJFQ
SSBQLZCPZUIJBQTPNVVVV
Il comporte ℓ = 964 caractères, un matériel suffisant pour appliquer les techniques décrites précédemment.

retour

Détermination de la longueur de clef k

Selon ces méthodes, nous commençons par décaler cycliquement le texte chiffré de 1, 2, ... 50 [1] positions vers la droite. Pour chaque décalage s, nous comptons le nombre de coïncidences cs entre le texte chiffré initial C et sa version décalée C(s). Nous dressons ensuite l'histogramme des valeurs de cs (en ordonnée) en fonction de s (en abscisse) :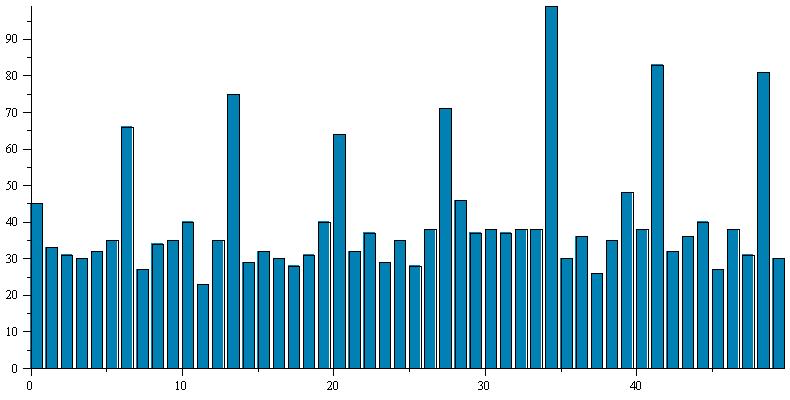


N'est-ce pas explicite ? Les nombres de coïncidences s'établissent en deux populations clairement distinctes :
  • des "petites valeurs" comprises entre 23 et 48 avec un écart-type de 5,382 et une moyenne de 34,186 ;
  • des "grandes valeurs" comprises entre 64 et 99 avec un écart-type de 12,014 et une moyenne de 77,000.
Ces valeurs sont en bon accord avec ℓ/26 = 37,077 et ℓ/12,878 = 74,859 respectivement.

Les "grandes valeurs" sont toutes obtenues pour des indices multiples de 7 !

La cause est entendue : notre mot-clef est de longueur k = 7.

retour

Détermination de la  1ère lettre du mot-clef

Nous formons le "sous-texte" obtenu en sélectionnant une lettre sur 7 du chiffré en partant de la 1ère, soit C1 = (C[7i+1])1≤i≤E((ℓ−1)/k). Ces lettres ont toutes été chiffrées à l'aide de la 1ère lettre du mot-clef  -- autant dire que ce sous-texte provient d'un chiffrage de César.

Nous lui appliquons une analyse des fréquences [2].

Voici l'histogramme obtenu (à gauche) avec pour référence l'histogramme de base (à droite) :

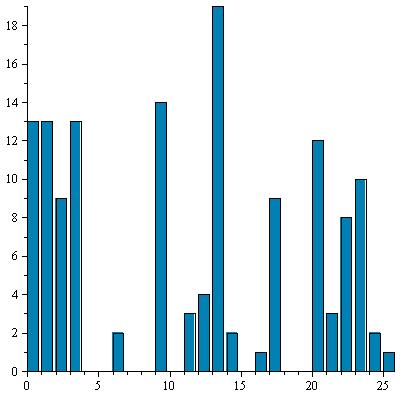
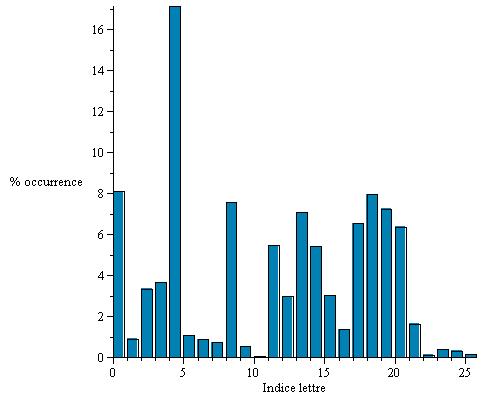
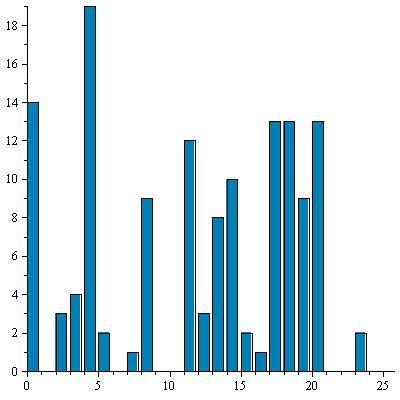
La ressemblance demande à être précisée. L'histogramme de gauche présente son plus grand pic à l'abscisse 13 (contre 4 dans l'histogramme de référence). Aussi faisons-nous subir à l'histogramme de gauche un décalage de 13−4 = 9 positions vers la gauche. Comparons à nouveau le résultat avec l'histogramme de référence :

Compte tenu de la brièveté du sous-texte étudié (137 caractères), nous considérons l'accord comme satisfaisant. Observons que toutes les caractéristiques de distribution signalées précédemment sont présentes. Nous concluons que la 1ère lettre du mot-clef est de rang alphabétique 9 (le "A" étant de rang 0).

Conclusion : le mot-clef commence par un "J".

retour

Détermination des lettres suivantes du mot-clef

On poursuit de même l'étude des autres sous-textes Cj = (C[7i+j])1≤i≤E((ℓ−j)/k) pour 2 ≤ j ≤ 7. Le décalage nécessaire est déterminé d'après l'abscisse du pic le plus élevé. Il est confirmé par la bonne corrélation entre l'histogramme décalé et la répartition de référence.

Les résultats sont présentés dans le tableau suivant :

j =
 histogramme brut
 décalage
 histogramme décalé
 jième lettre
2
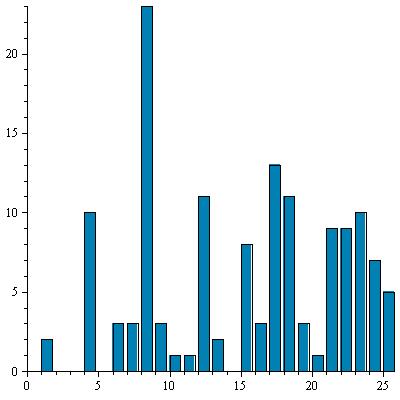4
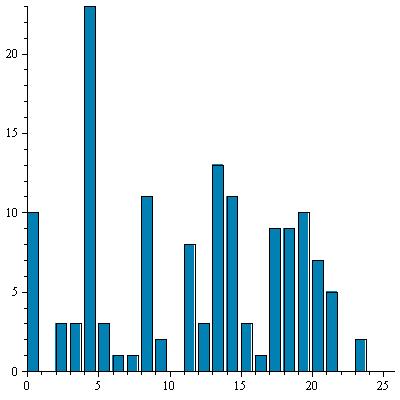E
3
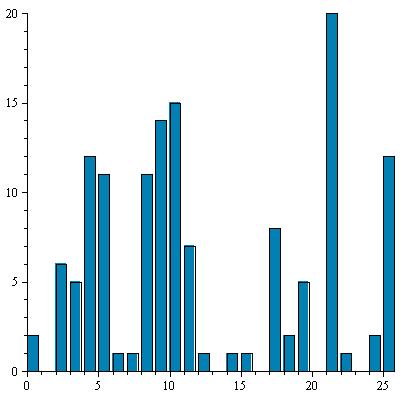17
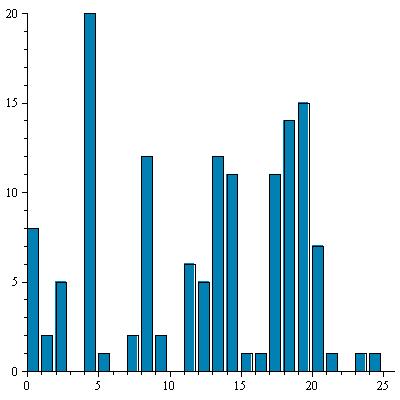 R
4
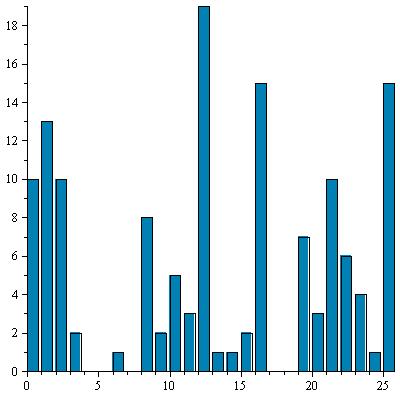 8
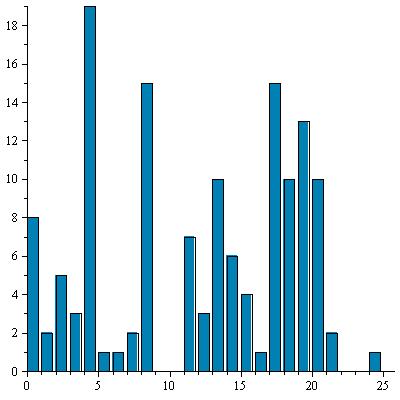 I
5
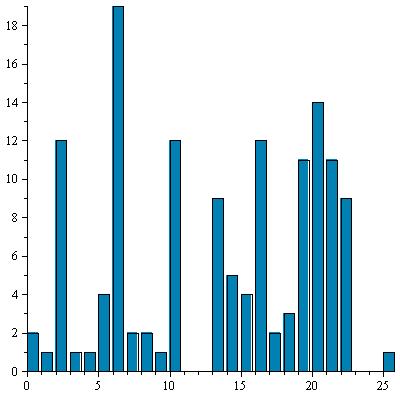 2
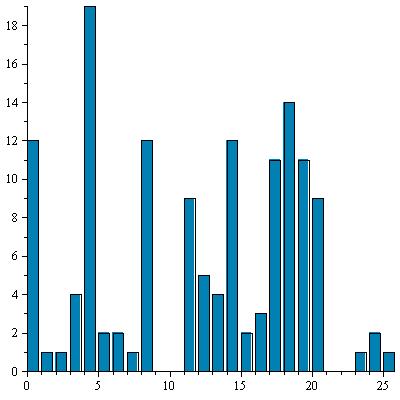 C
6
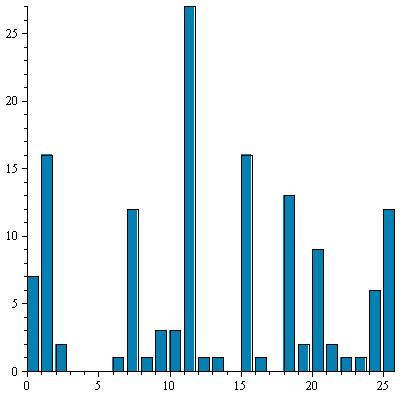 7
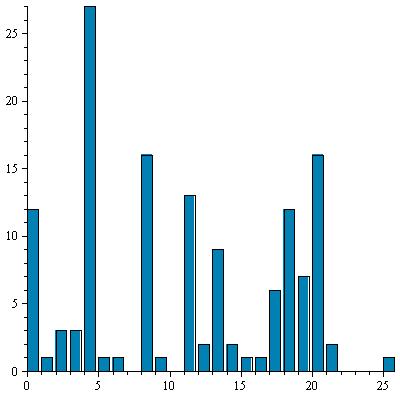 H
7
 14
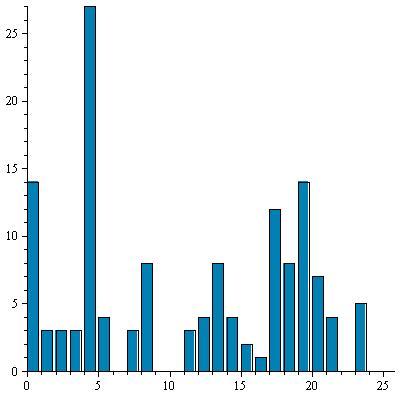 O

Conclusion : le mot-clef est "JERICHO".

retour

Décryptage

Il est alors trivial de reconstituer le clair. On effectue simplement la soustraction modulaire du chiffré avec le mot-clef concaténé à lui-même autant de fois que nécessaire.

Voici le résultat  (où les espaces ont été rajoutées pour la lisibilité du beau texte de V. Hugo [Les Châtiments]) : 
sonnez sonnez toujours clairons de la pensee
quand josue reveur la tete aux cieux dressee
suivi des siens marchait et prophete irrite
sonnait de la trompette autour de la cite
au premier tour qu il fit le roi se mit a rire
au second tour riant toujours il lui fit dire
crois tu donc renverser ma ville avec du vent
a la troisieme fois l arche allait en avant
puis les trompettes puis toute l armee en marche
et les petits enfants venaient cracher sur l arche
et soufflant dans leur trompe imitaient le clairon
au quatrieme tour bravant les fils d aaron
entre les vieux creneaux tout brunis par la rouille
les femmes s asseyaient en filant leur quenouille
et se moquaient jetant des pierres aux hebreux
a la cinquieme fois sur ces murs tenebreux
aveugles et boiteux vinrent et leurs huees
raillaient le noir clairon sonnant sous les nuees
a la sixieme fois sur sa tour de granit
si haute qu au sommet l aigle faisait son nid
si dure que l eclair l eut en vain foudroyee
le roi revint riant a gorge deployee
et cria ces hebreux sont bons musiciens
autour du roi joyeux riaient tous les anciens
qui le soir sont assis au temple et deliberent
a la septieme fois les murailles tomberent
... tout comme est tombé le message chiffré en Vigenère après que la septième lettre du mot-clef ait été déterminée !

retour

Conclusion

Historiquement, les attaques initiales sur le Vigenère ont été menées "à la main". Ici, bien évidemment, nous avons eu recours à l'ordinateur pour dénombrer les auto-coïncidences et tracer les histogrammes correspondants. L'ensemble du processus pourrait d'ailleurs être largement automatisé. D'évidence, le Vigenère n'est plus le "chiffre indéchiffrable" qu'il semblait à son invention.

Bien sûr, les substitutions polyalphabétiques ont connu des raffinements depuis le Vigenère. La mécanisation des processus de (dé)chiffrage a connu son apogée au tournant de la seconde guerre mondiale. Nous décrivons par ailleurs l'exemple remarquable de la machine ENIGMA allemande, ainsi que les efforts accomplis pour décrypter ses messages.

Dans cette course au calcul, pour prendre les décrypteurs de vitesse, le recours à des systèmes de chiffrage résolument nouveaux s'imposait.

retour

Notes

[1]  Cette valeur est arbitraire ; nous parions sur une clef de longueur k < 50.

[2]  Celle-ci fonctionne, parce que l'extraction d'une lettre sur k dans un message chiffré monoalphabétiquement ne modifie pas globalement l'histogramme des fréquences, si le message d'origine est suffisamment long.