Accueilretour

Généralités ; notations

Généralités

cryptologie...

personnages

notations

usages

maths

Stéganographie

Cryptanalyse

Littérature

Transpositions

Subs. monoα

Subs. polyα 1 - 2

One-time pad

DES 1 - 2

Clef publique

Knapsack

Diffie-Hellman

RSA 1 - 2

Grands noms

Références



 Nous nous efforcerons de respecter les conventions et notations suivantes, à commencer par la terminologie.

Cryptologie, cryptographie et cryptanalyse

Sur le vocabulaire, il convient d'être précis. Dans notre Littré préféré, on trouve déjà la distinction entre
  • le déchiffreur, "personne qui a la clé d'un chiffre" ;
  • tandis que décrypter, c'est "trouver le code permettant de déchiffrer".
Dans le second cas, il est implicite que ce code n'était pas détenu a priori par le décrypteur.

Dans une conception plus moderne, nous adoptons les définitions suivantes :

La cryptographie est l'ensemble des techniques permettant de réaliser les deux buts fondamentaux suivants :
  • transmission confidentielle de données ;
  • détection de captage ou de modification non autorisée ou malveillante lors du transfert.
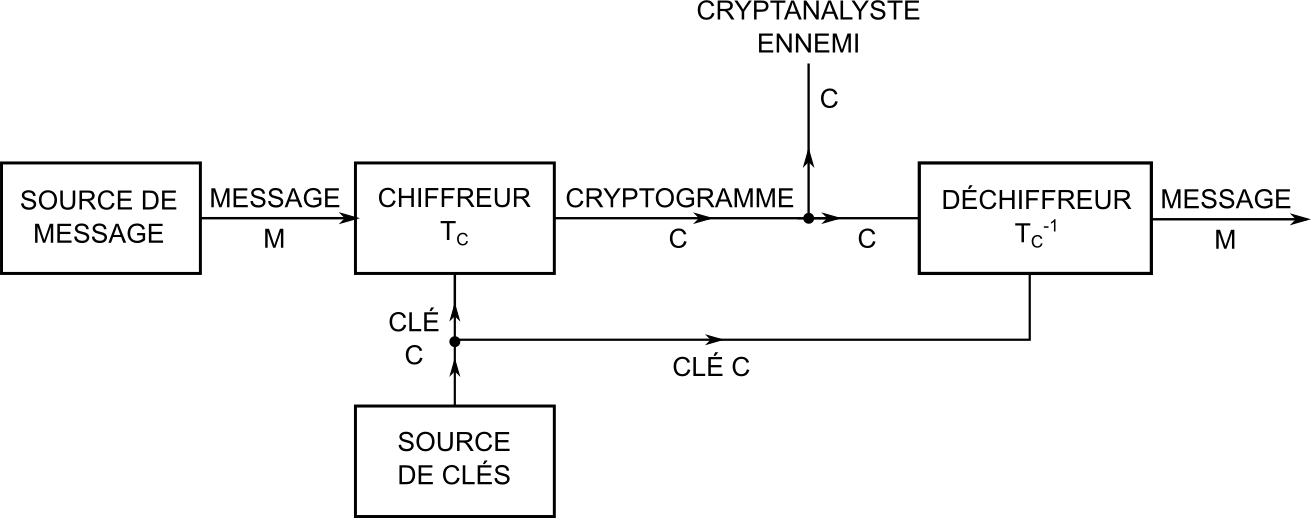
En 1949, le génial mathématicien Claude Shannon (père de la théorie de l'information) publie un article d'une importance fondamentale, Théorie de la communication des systèmes secrets, où il résume ainsi les éléments avant de les théoriser :

(traduction du schéma original de C. Shannon)

La cryptanalyse en revanche est l'ensemble des méthodes par lequel le cryptanalyste ("l'ennemi"), peut
  • briser le chiffrage et accéder à la signification du message (avec ou sans détermination de la clé) ;
  • s'immiscer dans le processus de chiffrage et diffuser des messages modifiés ou faux.
La cryptologie consiste en l'étude globale des deux disciplines ; elle s'intéresse conjointement aux ressources de chiffrage et aux moyens de les percer.

retour

Les personnages

Pour personnifier les protagonistes qui s'échangent des messages chiffrés, il est d'usage d'utiliser les prénoms d'Alice et Bob (plutôt que les lettres A et B).

L'ennemi (cryptanalyste) est désigné par Eve. C'est une allusion au terme anglais désignant l'activité d'espionnage, eavesdropping, dont l'étymologie est d'ailleurs assez alambiquée...

Notations

On peut classer les systèmes de cryptage en deux types principaux.
  • dans un cryptage symétrique, la clé (donnée permettant le chiffrage) est unique. Elle sert aussi bien pour le chiffrage que le déchiffrage.
  • dans un cryptage asymétrique, il existe deux clés. La clé publique permet à tout un chacun de chiffrer à destination d'un destinataire donné. Mais seule la clé privée de ce dernier lui permettra d'effectuer le déchiffrage [cf. "clef publique"]
Dans les systèmes de cryptages historiques, les messages (même chiffrés) circulaient exclusivement sous forme littérale. Dans les systèmes contemporains, les textes sont d'abord convertis en nombres entiers (p. ex. grâce au code ASCII). C'est sur ces derniers que s'effectuent les opérations de chiffrage, qui sont essentiellement des calculs.

L'alphabet 𝒜 sera, dans le premier cas, {A, ..., Z} ; dans le second, {0, 1}. Si l'alphabet utilisé pour les messages chiffrés n'est pas le même que celui des messages clairs [1], nous le noterons 𝒜'.

On notera d'autre part :
  • M le message (en clair), et m sa conversion en nombre entier, le cas échéant ;
  • C le chiffré (texte crypté), et c sa conversion en nombre s'il y a lieu.
  • ℓ désignera si besoin la longueur du message (ou du chiffré).
Lorsque M (resp. C) décrit toutes les possibilités, on parlera de
  • l'espace des messages clairs  ℳ = 𝒜 ℓ [2] ;
  • l'espace des messages chiffrés 𝒞 = 𝒜' ℓ -- l'alphabet correspondant aux messages chiffrés n'étant pas nécessairement le même que celui utilisé pour les messages clairs ;
  • l'espace des clés 𝒦.

us et coutumes

Il est d'usage en cryptographie d'écrire en minuscules le clair et en majuscules le CHIFFRÉ.

Ceci permet de noter commodément des décryptages partiels : ainsi dans XaYeZ, les 2ème et 4ème lettres du mot ont été identifiées.

Dans les substitutions monoalphabétiques, s'il est acquis que la lettre X chiffre y, on note éventuellement X =̂ y [3].

Enfin, on omet généralement les ponctuations, espaces et accents dans le clair avant d'appliquer le système de cryptage. Le contexte permet de retrouver le sens. Cependant, certains systèmes nécessitent d'incorporer et de chiffrer la ponctuation (nous le signalerons).

retour

Notions mathématiques

Les cryptosystèmes actuels, on l'a dit, traitent des nombre plutôt que des mots. Les notions mathématiques suivantes interviennent à l'occasion dans leur construction. Elles facilitent également leur compréhension et leur étude.

  • Le PGCD de deux entiers m et n  est noté m∧n.
  • Le groupe cyclique fini d'ordre n est noté ℤ/nℤ = {0̅, 1̅, ..., n̅−̅1̅}. On utilisera particulièrement les valeurs n = 26 (correspondant à l'alphabet) et n = 2 (dans le cas d'un chiffrage arithmétique sur un clair écrit en binaire). Nous notons ⊕ l'addition modulo n ; le cas échéant, ⊖ la soustraction modulo n (pour  n = 2, ces deux opérations coïncident).
  • Lorsque p est un entier premier, ℤ/pℤ est un corps : "le" corps fini à p éléments, aussi noté 𝔽p.
  • Le (petit !) théorème de Fermat énonce que pour tout entier non nul a et pour tout entier premier p, ap−1 ≡ 1 [mod p].
  • L'indicateur d'Euler φ(n) d'un entier n est le nombre d'entiers > 0 premiers avec n : φ(n) = card(k | 0 < k < n et k∧n = 1). φ est partiellement multiplicatif dans le sens suivant : si  m∧n = 1 alors φ(mn) = φ(m)φ(n). Ceci permet de calculer, à partir de φ(p) = p−1 si p est premier, et plus généralement φ(pk) = pk−pk−1= pk(1−1/p), la valeur de φ(n) si la décomposition de n comporte les facteurs premiers p1, ..., pk : φ(n) = n∏i=1k(1−1/pi).

  • Le théorème des restes chinois énonce que, pour tout p-uplet (n1, ... np) d'entiers premiers entre eux deux à deux (i≠j ⇒ ni∧nj = 1), le système de congruences (x ≡ ai mod. ni)1≤i≤p admet une unique solution mod. ∏i=1pni .
retour

Notes

[1]  cas d'un codage numérique

[2]  Il s'agit là d'une borne supérieure ; toutes les possibilités ne sont pas présentes.

[3]  une notation empruntée à F. L. Bauer