Accueilretour

Systèmes modernes à clé secrète

2. D.E.S. (Data Encryption System) (1)

Généralités

Stéganographie

Cryptanalyse

Littérature

Transpositions

Subs. monoα

Subs. polyα 1 - 2

One-time pad

DES 1 - 2

brève histoire

principe

décryptage

détails

fonction f
S-boîtes
sous-clefs

avantages

faiblesses

Clef publique

Knapsack

Diffie-Hellman

RSA 1 - 2

Grands noms

Références

Une brève histoire du DES

À la fin des années 60, la société IBM travaillait sur un système de cryptage nommé LUCIFER. Elle consulta, entre autres, l'agence de sécurité NSA pour des conseils techniques. Dans la conception de LUCIFER, beaucoup ont vu la patte de Claude Shannon himself.

LUCIFER évolua pour devenir le système DES qui fut proposé à l'organisation NBS (National Bureau of Standards [1]) comme nouveau standard national de cryptage.

En 1977, le NBS entérina le choix du DES comme norme de cryptage pour les "unclassified computer data" en publiant la recommandation FIPS 46.

Le DES demeura en usage jusqu'au tournant du XXème siècle. En 1997, le NIST (ex-NBS) lança un appel visant à lui trouver un successeur. Ceci devait déboucher sur l'AES (Advanced Encryption System).

retour

Principe général

Le DES, comme tous les cryptages modernes, nécessite la transcription binaire du message (au moyen du code ASCII). Nous notons toujours "⊕" l'addition modulo 2 bit par bit (ou XOR).

DES emploie une clef de 8 octets soit 64 bits dont 8 servent au contrôle de parité. Il reste donc 56 bits utiles.

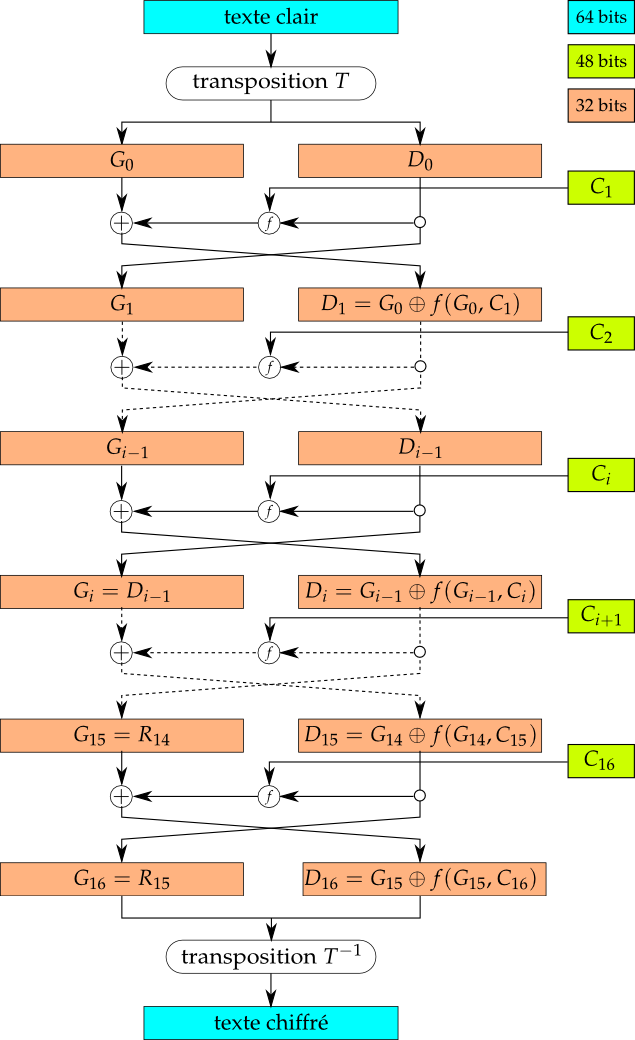
Le texte clair est découpé en blocs de 8 octets. Chaque bloc subit les transformations suivantes (cf. schéma ci-après) :
  • une transposition T -- indépendante de la clef.
  • une séparation en deux moitiés Gauche et Droite (de 32 bits chacune, donc) :
    G0
    		 D0
  • 16 étapes de cryptage selon le principe suivant (la fonction f et la sous-clef Ci sont détaillées plus loin) :
    ⎧
    ⎨
    ⎩
    Gi =
    		 Di−1
    Di  = 
    		Gi−1 ⊕ f(Di−1, Ci)
  • la transposition inverse T−1.
Sous une forme plus synthétique :

DES = T−1◦h16 ◦∏i=115(g◦h16−i )◦T

où

hi : (G, D) ↦ (G ⊕ f(D, Ci))
g  : (G, D) ↦ (D, G)

Ceci peut se schématiser ainsi :



retour

Décryptage

Il est particulièrement simple ! Les opérations hi et g étant involutives [2], il suffit d'appliquer la même procédure en inversant l'ordre des sous-clefs. Ainsi, alors que

DES = T−1◦h16 ◦g◦h15◦g...◦h2◦g◦h1◦T

tout simplement :

DES−1 = T−1◦h1 ◦g◦h2◦g◦...◦h15◦g◦h16◦T

Voilà !

retour

Détails

Précisons maintenant la fameuse fonction f et la construction des sous-clefs Ci à partir de la clef d'origine.

fonction f

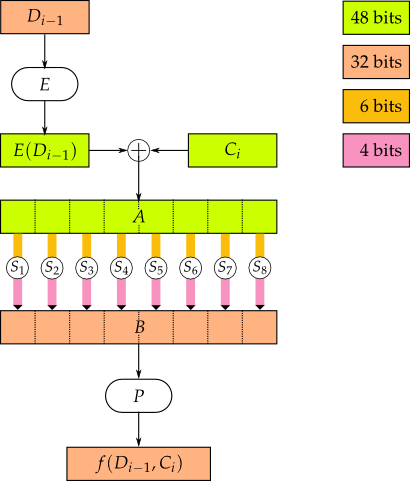
Partons d'un bloc de 32 bits Di−1. La fonction f consiste à lui appliquer les transformations suivantes :
  • expansion à 48 bits (E(Di−1)) par duplication de certains bits ;
  • ajout modulo 2 (⊕) avec Ci  (chaîne A) ;
  • découpage de A en 8 groupes de 6 bits ;
  • application à chacun d'entre eux d'un des 8 modules de substitution Si ("S-boîtes", voir plus loin) sortant sur 4 bits ;
  • concaténation en une nouvelle chaîne de 32 bits ;
  • application d'une permutation P finale ("P-boîte").
On peut se référer au schéma suivant :



retour

S-boîtes

Expliquons encore le fonctionnement des S-boîtes. Elles acceptent 6 bits en entrée, sortant sur 4. D'une chaîne d'entrée b1b2b3b4b5b6, on isole les 2 bits extrêmes b1b6 et les 4 du milieu b2b3b4b5, obtenant 2 entiers, respectivement, de 0 à 3 et de 0 à 15. Le premier est introduit en ordonnée, le second en abscisse dans un tableau à double entrée comme le suivant :
b2b3b4b5


0
 1
 2
  3
 4
 5
 6
 7
 8
 9
 10
 11
 12
 13
 14
 15
b1b6 0
 14
 4
 13
 1
 2
 15
 11
 8
 3
 10
 6
 12
 5
 9
 0
 7
1
 0
 15
 7
 4
 14
 2
 13
 1
 10
 6
 12
 11
 9
 5
 3
 8
2
 4
 1
 14
 8
 13
 6
 2
 11
 15
 12
 9
 7
 3
 10
 5
 0
3
 15
 12
 8
 2
 4
 9
 1
 7
 5
 11
 3
 14
 10
 0
 6
 13

(C'est la S-boîte n°1, S1 que nous avons reproduite ci-dessus).

retour

construction des sous-clefs

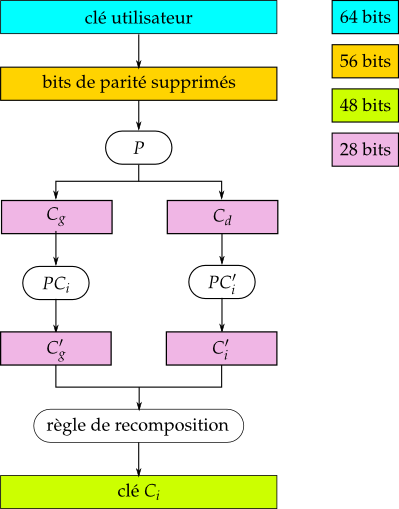
  • La clef-utilisateur de 64 bits est d'abord expurgée de ses bits de parité (→ 56 bits).
  • Elle subit une permutation P avant d'être scindée en 2 blocs de 28 bits.
  • Chacun subit une permutation circulaire distincte, qui dépend également de l'indice i de la sous-clef.
  • Les deux blocs obtenus sont recomposés (et non concaténés).
Le résultat est la sous-clef Ci . Le schéma ci-dessous récapitule le processus.


retour

Avantages du DES

Le cryptage DES s'accompagne d'un "effet avalanche". Une petite modification du clair se traduit, au bout des 16 étapes de cryptage, par un changement de plus de 50% du chiffré.

Le DES est rapide à calculer. Les opérations se résument à des permutations et des additions modulaires. C'est un critère qui fut jugé important au moment de son apparition. Les possibilités de calcul fournies par l'électronique étaient alors très inférieurs à leur niveau actuel.

Le DES a donc malgré tout permis dès le début des années 80 la réalisation de puces de (dé)chiffrage comme celle-ci  (Crypto AG) :


Il s'agissait de circuits de haute fiabilité (avec un MTBF [3] très élevé), mais néanmoins suffisamment rapides pour chiffrer / déchiffrer à la vitesse d'environ 20 Mbits/s.

retour

Faiblesses et attaques sur le DES

  • Dans son mode le plus simple (1 seule étape), le DES est monoalphabétique...
  • L'espace des clefs 𝒦 est relativement réduit : #𝒦 = 256 -- ce qui a fini par devenir insuffisant.
  • Les S-boîtes, essentielles pour sa sécurité, sont longtemps demeurées secrètes, mais ont finalement été publiées.
  • La fonction f recelait un certain nombre de trappes. Aucune n'a toutefois été rendue publique.
  • Des propriétés surprenantes du chiffrage DES ont été découvertes a posteriori. Par exemple, une symétrie par complémentation (0 ↔ 1) du clair et de la clef se propage au chiffré...
Voyons maintenant comment le DES dut laisser sa place...

retour

Notes

[1]  maintenant NIST (National Institute of Standards and Technology)

[2]  càd, si l'on applique 2 fois hi (resp. g), on retrouve l'identité.

[3]  Mean Time Between Failures