Accueilretour

Systèmes historiques

3. substitutions polyalphabétiques (1)

Généralités

Stéganographie

Cryptanalyse

Littérature

Transpositions

Subs. monoα

Subs. polyα 1 - 2

Vigenere

exemple

analyse

méthode récente

One-time pad

DES 1 - 2

Clef publique

Knapsack

Diffie-Hellman

RSA 1 - 2

Grands noms

Références



 Dans une substitution polyalphabétique, le passage du clair au chiffré résulte toujours d'un procédé arithmétique. Mais ici, une lettre donnée, disons a, du clair, peut être rendue par différentes lettres dans le chiffré.

Une telle substitution modifie donc globalement la répartition des lettres (bigrammes, trigrammes...) dans le chiffré -- plutôt que de simplement la décaler ou la permuter. Les fréquences sont uniformisées. L'histogramme de départ ne peut pas être reconstitué simplement. L'analyse des fréquences est ainsi compliquée, voire impossible (cf. One-time pad).

Ce type de système remonte au XVIème siècle. Il a connu son apogée au milieu du XXème siècle avec l'apparition de machine électromécaniques (la plus connue étant ENIGMA) réalisant des cryptages de ce type souvent très élaborés.

Nous préférons étudier en détail les forces et faiblesses du système original :

Le cryptage Vigenère

Le principe du cryptage Vigenère est souvent présenté sous forme d'un tableau à double entrée qui donne une idée faussement complexe du système. Il s'agit d'une simple addition modulo 26 du clair avec un mot-clef que l'on répète pour atteindre la longueur du clair :

chiffré = clair ⊕ (clef)p

où p est suffisamment grand pour que la répétition de la clef "couvre" la totalité du clair. La dernière occurrence de la clef est tronquée si nécessaire.

Exemple

Les lettres sont indexées de 0 à 25. Le mot-clef est CLE. Le clair est "Tout va bien".

clair
 t
 o
 u
 t
 v
 a
 b
 i
 e
 n
index (clair)
 19
 14
 20
 19
 21
 0
 1
 8
 4
 13
clef
 C
 L
 E
 C
 L
 E
 C
 L
 E
 C
index (clef)
 2
 11
 4
 2
 11
 4
 2
 11
 4
 1
index (chiffré)
 21
 25
 24
 21
 6
 4
 3
 19
 8
 14
chiffré
 V
 Z
 Y
 V
 G
 E
 D
 T
 I
 P

retour

Remarque

Les cryptages de type "César" sont des cas particuliers du cryptage Vigenère pour lesquels la clef est de longueur 1. Par exemple, le "César" original (décalage de 3 unités) est le Vigenère de clef "D", tandis que le ROT13 correspond à la clef "N". Choisir une clef de longueur 1 ne présente donc aucun intérêt. Plus généralement, nous le verrons, le Vigenère est d'autant plus efficace que la clef est longue par rapport au clair.

Analyse

Le cryptage Vigenère aplanit le graphe des fréquences. Voici à titre d'exemple l'histogramme d'un texte chiffré qui va nous servir un peu plus loin d'exemple de cryptanalyse :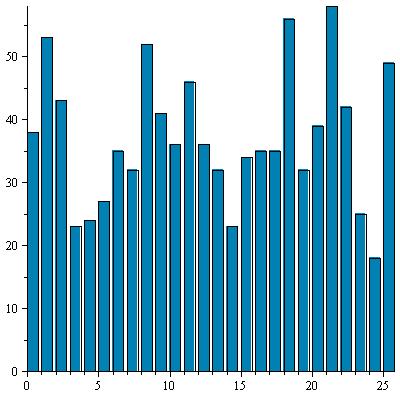

Bien qu'il s'applique à un texte de longueur modeste, cet histogramme ne présente aucune fréquence nettement prédominante. On le comparera avec profit avec l'histogramme de référence : ici, les fréquences sont resserrées ; leur écart-type est d'environ 1,108. Dans l'histogramme de référence, il est de 3,959. Comment procéder alors ?

Le point faible du Vigenère est la répétition de la clef. Si celle-ci est de longueur k, on peut subdiviser le chiffré en k  "sous-chiffrés" Cj (0 ≤ j < k) formés des caractères d'indices ≡ j [k]. Chacun d'entre eux a été chiffré grâce à une seule lettre de la clef, donc selon un simple chiffre de César.

Il est donc crucial de déterminer la longueur k de la clef. Comment réaliser ceci ?

La méthode "historique" a consisté en l'étude des répétitions au sein du message chiffré. Nous en avons donné un aperçu ici. Nous préférons présenter le point de vue actuel.

retour

méthode récente : coïncidences

"Récente" est à relativiser. Plus aucun cryptage de type Vigenère n'est utilisé actuellement. Mais cette méthode, perfectionnée, est à la base du décryptage des machines utilisées pendant et après la 2nde guerre mondiale, à commencer par l'ENIGMA.

Présentons ici les remarques théoriques avant de les appliquer à un exemple concret.

1. probabilité de coïncidence pour un texte aléatoire

Soient deux textes aléatoires (chaque caractère de l'alphabet y apparaît avec la même probabilité, donc 1/26) :

c1c2c3 ... ... cncn+1 ...
d1d2d3 ... ... dndn+1 ...

Nous étudions la probabilité de coïncidence de deux caractères de même indice (cn = dn). Celle-ci vaut :

Pa = p(cn = dn) = ∑x=az p(cn = x = dn) =  ∑x=az p(cn = x)² = ∑x=az (1/26)² = 26×(1/26)² = 1/26 ≃ 0,03846

2. probabilité de coïncidence pour un texte en langage courant

Supposons maintenant que les deux textes ci-dessus soient en langage courant (français). Le calcul de la probabilité de coïncidence est modifié du fait que les caractères ne sont plus équiprobables. Elle devient :

Pc = p(cn = dn) = ∑x=az p(cn = x = dn) =  ∑x=az p(cn = x)² ≃ 0,07765 ≃ 1/12,878 (≃ 1/13),

cette dernière valeur étant calculée d'après l'histogramme de référence. Elle est donc, empiriquement, plus du double de Pa. En revanche, le fait qu'elle soit supérieure résulte de l'inégalité de Schwarz de l'algèbre bilinéaire. En effet, notons l'alphabet (x1, ..., xN) et pi la probabilité d'occurrence du caractère xi . Soient U = (1, ..., 1) ∈ ℝN et P le vecteur (p1, ..., pN) (donc : ∑i=1Npi = 1 et ∑i=1Npi2 = Pc).  Alors

1 = ∑i=1Npi = ∑i=1Npi .1 = (P | U) (produit scalaire canonique des vecteurs P et U)

   ≤ ||P||.||U|| (Schwarz)

   = (∑i=1Npi2)1/2(∑i=1N12)1/2 =  √Pc√N

donc Pc ≥ 1/N = 1/26, l'égalité n'étant possible que si les vecteurs P et U sont colinéaires -- ce qui signifierait que tous les caractères xi ont la même probabilité (cas d'un texte aléatoire).

Ceci ne se produit jamais dans un langage courant, où la probabilité de coïncidence sera donc toujours supérieure.

3. probabilité d'auto-coïncidence dans un texte décalé

On reprend les notations générales : M  pour le message clair, C pour le chiffré. On décale cycliquement le clair et le chiffré de i positions vers la droite (p. ex.), notant M(i) et C(i) les résultats respectifs des décalages. On étudie ensuite les coïncidences avec les textes originaux.

Si i est "quelconque", C(i) est (pseudo-)aléatoire par rapport à C, donc on observe :

P(coïncidence C/C(i)) ≃ 1/26 (cas 1.)

Si en revanche i est la longueur k de la clef (ou un multiple de k), on montre alors :

théorème : P(coïncidence C/C(k)) = P(coïncidence M/M(k))

preuve. Supposons qu'on observe une coïncidence du caractère x entre le clair M et son décalé M(k), en position i. Cela signifie que x  se situe dans M en positions i et i−k. Ces deux occurrences de x  distantes de k sont chiffrées avec la même lettre du mot-clef [1], disons y. Appelons z le caractère résultant : z se situe donc en positions i et i−k dans C. Donc une coïncidence (de z) se produit entre C et C(k) (en position i). La réciproque s'obtient de même en inversant l'argument.

Maintenant, le clair M et sa version décalée M(k) sont en langage courant, donc on observe cette fois :

P(coïncidence C/C(k)) ≃ 1/13 (cas 2.)

(ou du moins, une augmentation sensible du taux de coïncidences).

L'application pratique, on va le voir, est d'une efficacité spectaculaire, et ne laisse aucune chance au chiffrage Vigenère.

retour

Note

[1]  Notons bien que cet argument ne tient que si i=k, ou un multiple de k.