



Systèmes historiques
2. substitutions monoalphabétiques
Généralités
Stéganographie
Cryptanalyse
Littérature
Transpositions
Subs. monoα
cryptage linéaire
César
ROT13
cryptage affine
analyse
conclusion
Subs. polyα 1 - 2
One-time pad
DES 1 - 2
Clef publique
Knapsack
Diffie-Hellman
RSA 1 - 2
Grands noms
Références
| f(code caractère clair) = code caractère chiffré |
On a donc le choix entre 26! ≃ 4,03.1026 permutations possibles [1], ce qui peut sembler considérable. Mais il faut trouver un moyen pratique et rapide d'effectuer le chiffrage (et le déchiffrage). Avec une permutation "quelconque", c'est la table complète de f qui doit être transmise entre le chiffreur et le déchiffreur. Si f est définie par une expression algébrique simple, il suffit de transmettre cette dernière.
On utilise des fonctions affines sur ℤ/26ℤ = {0̅, 1̅, ..., 2̅5̅}, de la forme x ↦ y = ax+b [26]. a et b doivent vérifier certaines propriétés que nous examinerons dans la version la plus générale.
Cryptage linéaire
C'est le cas le plus simple : a = 1. Il s'agit donc d'un simple décalage arithmétique de l'alphabet. Il n'y a que 25 possibilités non triviales, donc le décryptage d'un message chiffré ainsi est trivial par recherche exhaustive. Mentionnons seulement deux exemples célèbres :"Jules César"
On dit que Jules César correspondait avec ses alliés en dissimulant ses messages par un décalage de 3 positions dans l'alphabet. Cela correspond donc au cas : a = 1 ; b = 3̅. La fonction de cryptage est x ↦ y = x+3̅ [26] ; la fonction de déchiffrage est x ↦ y = x−3̅ [26]Par extension, les 25 chiffrages affines possibles sont tous désignés du nom de chiffres de César.
L'un d'entre eux a conquis une popularité récente avec l'apparition d'Internet.
ROT13
Le chiffrage ROT13 correspond à a = 1 et b = 1̅3̅. Son avantage ne réside pas dans une meilleure sécurité. Mais la même fonction sert au chiffrage et au déchiffrage. En effet, f : x ↦ y = x+1̅3̅ [26] est une involution [2] de ℤ/26ℤ, puisque 2×1̅3̅ = 2̅6̅ = 0̅ [26].Non seulement cette fonction est très facile à programmer, mais il n'y a rien d'autre à faire ! Sous Linux, la simple ligne
| alias rot13="tr '[A-Za-z]' '[N-ZA-Mn-za-m]'" |
réalise cette fonction.
C'est pourquoi ROT13 est couramment utilisé sur le net comme protection (faible) du contenu d'un message
- soit parce qu'il est d'une teneur ou d'une formulation un peu "crue" ;
- soit parce qu'il ne doit pas être découvert immédiatement (solution d'un casse-tête...) -- spoiler protection.
elementairemoncherwatson
On obtient :
RYRZRAGNVERZBAPUREJNGFBA
Ce court chiffré contient néanmoins 5 fois la lettre "R", soit plus de 20,8%... On se doute qu'une analyse de fréquences en viendrait trivialement à bout : avec un cryptage linéaire, dès que b est déterminé, tout est fini !
Aussi donnerons-nous un exemple de cryptanalyse sur un cas un peu plus consistant (?)

Cryptage affine
On revient à une fonction affine générale f : x ↦ y = ax+b [26]. f doit être injective (deux lettres distinctes du clair doivent rester distinctes dans le chiffré), donc bijective. Cela exige que a soit premier avec 26 (a∧26 = 1). Comme 26 = 2×13, l'indicateur d'Euler de 26 est φ(26) = (2−1)×(13−1) = 12. Il n'y a donc que 12 possibilités pour a, alors que b demeure quelconque dans {0̅, 1̅, ..., 2̅5̅}. Cela ne fait jamais que 12×26 possibilités (dont l'identité). C'est 12 fois plus que dans le cas des César, mais on est très loin de réaliser ainsi les 26! permutations possibles. Seule la facilité de calcul de f peut justifier une telle restriction.Exemple
Effectuons le cryptage affine au moyen de la clé (a, b) = (7, 1̅7̅) du clair suivant :maitrecorbeausurunarbreperchetenaitensonbecunfromage
Pour faciliter le chiffrage, tabulons la fonction f : x ↦ y = 7x+1̅7̅ [26] :
| clair |
a |
b |
c |
d |
e |
f |
g |
h |
i |
j |
k |
l |
m |
n |
o |
p |
q |
r |
s |
t |
u |
v |
w |
x |
y |
z |
| x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
| f(x) |
17 |
24 |
5 |
12 |
19 |
0 |
7 |
14 |
21 |
2 |
9 |
16 |
23 |
4 |
11 |
18 |
25 |
6 |
13 |
20 |
1 |
8 |
15 |
22 |
3 |
10 |
| chiffré |
R |
Y |
F |
M |
T |
A |
H |
O |
V |
C |
J |
Q |
X |
E |
L |
S |
Z |
G |
N |
U |
B |
I |
P |
W |
D |
K |
On obtient donc :
XRVUGTFLGYTRBNBGBERGYGTSTGFOTUTERVUTENLEYTFBEAGLXRHT
C'est sur ce message chiffré "inconnu" que nous allons nous livrer à une petite cryptanalyse.

Analyse
Il s'agit tout bonnement de déterminer la fonction f. On se reportera avec profit à l'histogramme de référence qui mesure la répartition des lettres en français.Dressons tout d'abord l'histogramme des fréquences du chiffré (les caractères sont indexés de 0 à 25) :
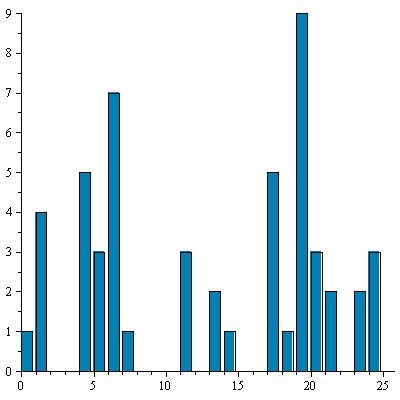
| f(4) = 19 = 4a+b [26] (1) |
Ensuite, les trois fréquences les plus élevées sont observées pour les indices 6, 4 et 17. Cela correspond aux caractères G, E et R. Les lettres suivant le e, par ordre décroissant d'occurrences, sont a, s, i, t, n... Il semble probable que le a soit chiffré par G, E ou R. Cela s'écrit :
| f(0) = 0a+b = b [26] ∈ {6, 4, 17}. |
Envisageons les 3 possibilités :
- b = 6 : revenant à (1), on déduit 1̅9̅ = 4a+6̅ [26] soit 4a = 1̅3̅ [26], ce qui est évidemment impossible (pour une question de parité).
- b = 4 : (1) donne alors 4a = 1̅5̅ [26], conduisant à la même impossibilité.
- b = 17 : c'est la seule possibilité restante !
|
g(y) = f-1(y) = 7̅-1(y−1̅7̅) = 15×(y+9̅) = 15y+1̅3̅5̅ = 15y+5̅ [26]. |
Il est alors facile d'appliquer g ainsi déterminée au chiffré. L'obtention d'un texte cohérent (le clair) validera la fonction obtenue.

Conclusion
Cette petite expérience illustre bien la faiblesse des substitutions monoalphabétiques. L'analyse des fréquences n'a porté que sur les 2 ou 3 caractères les plus rencontrés. Pour déterminer l'inverse de la fonction f, il a suffi de s'aider un peu de l'aspect mathématique. Mais on n'a même pas pris en compte que le clair fasse sens !Comme l'a dit D. Kahn :
"No monoalphabetic substitution can preserve security under heavy traffic. "
Notes
[1] moins l'identité[2] càd que f◦f = Idℤ/26ℤ -- c'est la seule involution non triviale de ℤ/26ℤ : il n'y a qu'un ROT13 !