Accueilretour
précédentsuivant

"Jardins d'Éden"

Origines

"Blinkers"

Jardins d'Éden

  Existence

  Inversibilité

Navires

Canons...

"Breeders"

Machines

Métacellules

Documents

 Calculer la génération suivante est facile. Quid du problème inverse ?

Existence des jardins d'Éden

On peut se demander si, étant donnée une génération, il est possible de lui trouver un antécédent, un "parent". Une hypothétique configuration sans parent est appelée jardin d'Éden [1]. Son existence, dans le cas d'un automate quelconque, est un problème ardu, nous allons y revenir.

Mais dans le cas du Jeu de la vie, un raisonnement combinatoire assez simple permet de conclure. Détaillons-le.
  1. Dans un carré 5×5, on construit facilement deux configurations donnant le même résultat. En effet, une unique cellule au centre donne un carré vide -- de même bien sûr qu'un carré initialement vide :

      ou →

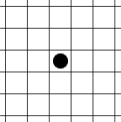  2. Supposons alors une configuration initiale contenue dans un carré de côté 5n−2. La notion de voisinage utile permet de limiter la recherche de ses antécédents à un carré de côté 5n :


    Celui-ci se décompose en n2 carrés de côté 5. Or nous avons trouvé deux configurations donnant le même résultat dans un tel carré. Donc le nombre de résultats possibles est majoré par 225−1 = 33 554 431. Pour l'ensemble du grand carré de côté 5n, cela fait donc (225−1)n² résultats différents au maximum pour la génération suivante.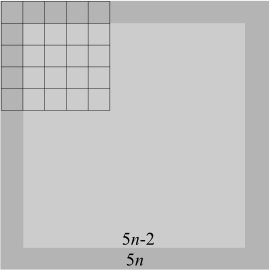
  3. Mais le carré de côté 5n−2 contient 2(5n−2)² configurations possibles.
  4. Or pour n assez grand, (225−1)n² < 2(5n−2)² [2]. Il y a donc plus de résultats possibles que de parents disponibles ; il doit donc exister des configurations sans parents [3].
Mais la construction explicite d'un jardin d'Éden est très délicate en raison du grand nombre de vérifications qu'elle exige. Le premier exemple connu a été construit en 1971 par R. Banks, il comporte 226 cellules et s'inscrit dans un rectangle 9×33 :

jardin d'Eden

Le plus petit actuellement connu a été découvert par N. Beluchenko en novembre 2009. Il comporte seulement 59 cellules dans un carré 11×11 :

jadrin d'Enen 2

On se rapproche là du minimum absolu réalisable. On sait en effet, grâce à des tests systématiques, que
  • toute configuration contenue dans une "bande" de largeur <5 possède un parent ;
  • de même que toute configuration incluse dans un rectangle 6×5.
Notons une question toujours ouverte : l'existence d'une configuration dotée d'un "père" mais sans "grand-père". On remarquera que ce n'est pas une conséquence triviale de la présence des jardins d'Éden. Il ne suffit pas de considérer la génération suivante d'un jardin d'Éden. Car en effet, elle pourrait fort bien être issue d'un autre parent, qui ne serait pas lui-même un jardin d'Éden...

haut de page

Inversibilité d'un automate cellulaire

Pour un automate cellulaire donné, un éventuel inverse serait un automate faisant passer d'une génération à la précédente. La question de l'existence d'un tel inverse est celle de la bijectivité de l'application qui fait passer d'une génération à la suivante. Elle pose deux conditions évidentes :
  • deux configurations distinctes doivent donner des générations filles distinctes (l'automate étudié doit être injectif) ;
  • il ne doit pas exister de jardin d'Éden, de configuration sans antécédent (l'automate doit être surjectif).
Deux conditions qui ne sont assurément pas vérifiées par le Jeu de la vie.

On dispose des résultats suivants :
  • le théorème de Moore-Myhill [4] énonce que pour un automate donné, un jardin d'Éden existe (non surjectivité) si et seulement si deux configurations donnent le même résultat (non injectivité) [5].
  • des résultats dus à Jarkko Kari (1992) établissent que le problème général de l'inversion d'un automate est indécidable [6].
La question de l'inversion des automates est donc un problème intrinsèquement difficile. Ceci laisse penser qu'un automate non inversible pourrait être appliqué à des questions de cryptage, comme "fonction à sens unique", remplaçant ainsi les fonctions arithmétiques habituellement utilisées dans les algorithmes type RSA. Des expériences ont déjà été menées dans ce sens [7].

haut de page

Notes

[1]  Cette terminologie date pratiquement de l'invention des automates cellulaires : elle est donc antérieure de 20 ans à la naissance du Jeu de la vie.

[2]  Cette inéquation est assez facile à résoudre, même avec une simple calculette, et donne n ≥ n0 = 465 163 192.

[3]  de moins de (5n0−2)2 = 5 409 419 870 487 457 764 cellules ! ...

[4]  datant du début des années 60, donc lui aussi bien antérieur au Jeu de la vie

[5]  Remarquons que ce n'est pas une conséquence triviale de l'équivalence bien connue entre injectivité et surjectivité pour une application d'un ensemble fini dans lui-même. En effet, l'ensemble des configurations possible d'un automate cellulaire est en général infini.

[6]  Il suffit qu'il utilise le voisinage standard de 8 cellules.

[7]  programme AUTOGEN, P. Mathieu (LIFL)

haut de page