Recouvreurs de plans
Origines
"Blinkers"
Jardins d'Éden
Navires
Canons...
"Breeders"
Space-fillers
Taux de croissance
Densité limite
Sawtooth
Croissances exotiques
Machines
Métacellules
Documents
Recouvreurs de plan (breeders,
space-fillers)
On nomme breeders ou
"recouvreurs de plan" (space-fillers)
des configurations qui non seulement croissent
indéfiniment, mais aussi ont une densité limite non
nulle. Elles tendent à occuper une proportion non négligeable de
l'espace.L'idée initiale pour les construire fut de fabriquer une sorte de super-puffer qui se déplacerait en émettant... des canons. Le nombre de ces canons augmentant linéairement dans le temps, et chacun d'eux émettant un train de glisseurs au même rythme, la croissance globale de la population serait quadratique ("en t2") -- bien le but poursuivi.
Dès 1970, ce schéma a été réalisé [1] grâce à une configuration de 4060 cellules. La partie principale se déplace en créant (à vitesse linéaire) des lance-glisseurs. Le taux de croissance est ainsi quadratique.
génération 2000 montrant le
train de canons lance-glisseurs

Taux de croissance
Il est facile de voir qu'on ne peut dépasser un taux d'accroissement quadratique (en t2). En effet, si la population initiale (t = 0) est contenue dans un carré de côté N0, celle de la génération t sera incluse dans un carré de côté N0 + 2t, donc son effectif sera majoré par (N0 + 2t)2 = 4t2 + 4N0t + N02, soit bien O(t2). Ce n'est donc pas compatible avec une croissance en tα avec α > 2.Densité limite
Ceci permet de définir rigoureusement la densité limite d'une population : on étudie la limite du rapport N(t)/(N0t2) si N(t) est la population après t générations et N0 = N(0) la population initiale.Pour une population stable (qui ne s'éteint pas), Noam Elkies a démontré en 1994 que cette limite vaut au maximum 1/2 sur l'espace plan tout entier. Mais cette valeur peut être (légèrement) dépassée si l'on se limite à un rectangle m×n : la borne supérieure théorique est alors de (mn + m + n)/(2mn) (M. Moore, 1995).
D'un autre côté, cette borne ne peut pas être atteinte pour tout (n,m). Par exemple, si n = m = 8, le majorant théorique est 5/8 = 0,625. Mais la plus grande valeur réalisable en pratique est 9/16 = 0,5625. Les solutions optimales ont ainsi été recherchées jusqu'à la taille 20×20.
"Dents de scie" (sawtooth)
Il ne faudrait pas croire que lorsqu'une population devient arbitrairement nombreuse, elle le fait obligatoirement de manière monotone (en étant croissante). Mathématiquement, la population peut être non bornée (majorée), mais sans avoir pour limite +∞.On nomme ces configurations "en dents de scie". La première d'entre elles a été réalisée en 1991 par D. Hickerson, à partir d'une population de 983 cellules. En voici succinctement le principe. La machine principale émet d'abord une lente (vitesse c/3) "tortue", puis un navire lourd suivi d'un train de navires légers. Ceux-ci avancent plus vite (vitesse c/2) que la tortue, qu'ils rattrapent...
les navires sur le point de rattraper la tortue
... La collision du navire lourd et de la tortue produit un "pain" (loaf) -- une configuration immobile. Celui-ci est percuté par les navires légers qui suivent, ce qui a pour effet... de la faire reculer [3] vers la machine principale. Quand elle a rejoint cette dernière, l'effectif est alors minimal (1212). À ce moment-là, un autre train mené par un navire lourd prend le départ, recommençant le cycle. Mais quand il rattrapera la tortue, celle-ci se sera éloignée, ce qui fait que le train total sera plus long. L'effectif atteindra ainsi un nouveau maximum absolu [4]. Le tracé de la population en fonction du temps justifie le nom :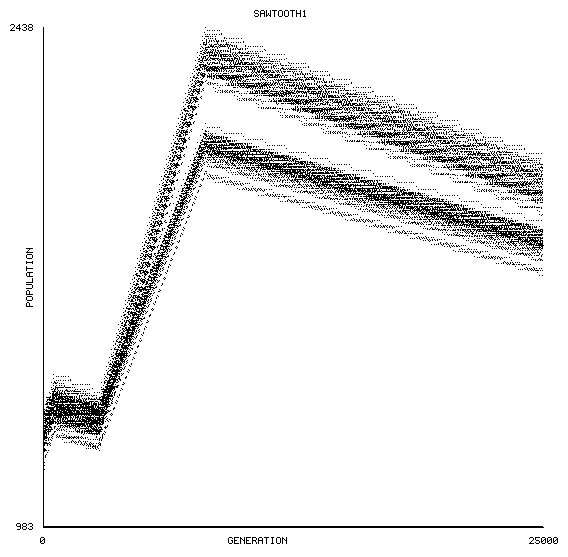
Notons que ces configurations ne recouvrent pas le plan. Leur densité limite est 0. Nous les présentons comme introduction à ce qui suit.
Croissances exotiques
À côté des taux d'accroissement classiques évoqués précédemment : en t (canons, puffers) et en t2 (breeders, space-fillers), on a obtenu toute une variété de croissances "exotiques" [5] :- en √t, en t√t et en t1/3 ;
- en ln(t) et (ln(t))2;
- en tln(t) et t(ln(t))2 ;
- en Kt avec K
= (3−√5̅)/4320, ou en Kt2
avec K = (π−2)/720.
Ces résultats ne constituent pas une surprise quand on connaît les résultats suivants.
Notes
[1] Devinez
par qui ? ...
... qui fonctionne sensiblement sur le même principe
[3] une bien étrange physique -- en fait, le résidu de la collision est un "pain" légèrement décalé vers l'arrière.
[4] population (21t+1+13159)/10 à la génération 18(21t) + 222
[5] qui se conforment toutes, bien sûr, à la contrainte du O(t2)
[6] π est bien sûr transcendant. Dans son cas, la formule utilisée est la relation de Leibniz π/4 = ∑n=1∞(−1)n/(2n+1) -- une série dont la lenteur désespérante de la convergence est quelque peu compensée par la vitesse des simulateurs du Jeu de la vie. Voici sa configuration initiale, qui comporte 3552 cellules :