



Le paradoxe de Bertrand
Sémantique
Logique
Infini
Mesure
Probas
Nombres
Physique
Soit un cercle de rayon R dans lequel nous prenons une corde au hasard. Quelle est la probabilité pour que la longueur de cette corde soit supérieure au côté du triangle équilatéral inscrit dans le cercle (... qui vaut combien, au fait) ?
Il y a plusieurs réponses !...
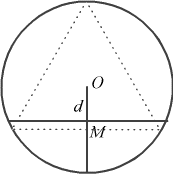
Argument 1 : La longueur de la corde est seulement fonction de la distance d de son milieu au centre du cercle. Disons que ce milieu M est pris sur un certain rayon du cercle et admettons que, sur ce rayon, la répartition du point M soit uniforme. Alors, la probabilité cherchée vaut 1/2, car les cas favorables correspondent à OM ≤ R/2 :
Argument 2 : Pour définir la corde, on fixe l'une de ses extrémités (A) et on fait varier l'autre (B) aléatoirement sur le cercle. En admettant une répartition uniforme du point B sur ledit cercle, la probabilité cherchée est dans ce cas 1/3 (un tiers des points B du cercle donnent lieu à un cas favorable) :

Argument 3 (avec le même schéma) : On considère la corde uniquement définie par sa longueur. Celle-ci peut prendre toute valeur entre 0 et 2R. Le cas du triangle équilatéral correspond à une longueur R√3̅. Notre corde a donc √3̅/2 chances d'être de longueur inférieure à la valeur fatidique. La probabilité que nous cherchons vaut donc ici 1−√3̅/2 ≃ 0,134.
Argument 4 : La corde est entièrement déterminée par la position de son milieu M à l'intérieur du disque. Si l'on admet maintenant que le point M est uniformément réparti dans le disque, alors la probabilité cherchée est ici égale à 1/4, les cas favorables étant ceux où M est situé à l'intérieur d'un disque de rayon R/2 :

Les résultats changent, mais demeurent divergents, si l'on remplace le "côté du triangle équilatéral inscrit" par toute autre longueur r∈]0,R[.
Le "paradoxe" n'est qu'apparent. Il tient à l'attribution d'une signification intrinsèque au terme probabilité. Il y a en fait quatre probabilités différentes ici, liées à quatre méthodes de mesure de la répartition d'une corde sur le cercle. Les quatre calculs sont justes, chacun étant fait dans le cadre d'un espace probabilisé bien spécifique.
D'après une entrée du Dictionnaire des mathématiques, A. Bouvier, M. George, F. Le Lionnais, PUF, 1979