Le problème de Kakeya

Sémantique

Logique

Infini

Mesure

Probas

Nombres

Physique

En 1917, le japonais Kakeya posa le problème suivant :

Trouver la figure d'aire minimale dans laquelle on puisse faire tourner de 2π un segment de longueur unité (une "aiguille"), d'un mouvement continu (pouvant comporter des translations).

Bien sûr, π/4 suffit clairement si l'on fait tourner l'aiguille autour de son centre. Mais cela ne nous mène pas bien loin.

Pendant un certain temps, on a cru que l'hypocycloïde à trois sommets convenait. C'est la figure décrite par un point d'un cercle qui roule sans glisser à l'intérieur d'un autre trois fois plus grand. L'aire ainsi obtenue est π/8 :

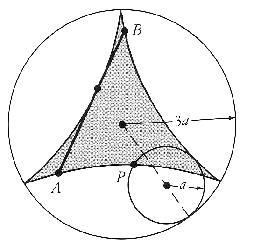
Toutefois, la réponse surprenante à la question fut apportée en 1928 par le mathématicien russe Besicovitch. En fait, Besicovitch étudiait une question semblable depuis plusieurs années déjà. Mais son pays était alors assez coupé du monde et il n'avait pas eu connaissance du problème de Kakeya.

L'aire minimale est... nulle. Plus rigoureusement, la borne inférieure des aires convenables est 0. On peut donc retourner l'aiguille en demandant que l'aire balayée soit arbitrairement petite. Pour construire un ensemble de mesure très réduite, à l'intérieur de laquelle l'aiguille peut faire demi-tour, on peut partir d'un triangle. On découpe celui-ci en tranches que l'on réarrange en les faisant se chevaucher beaucoup :

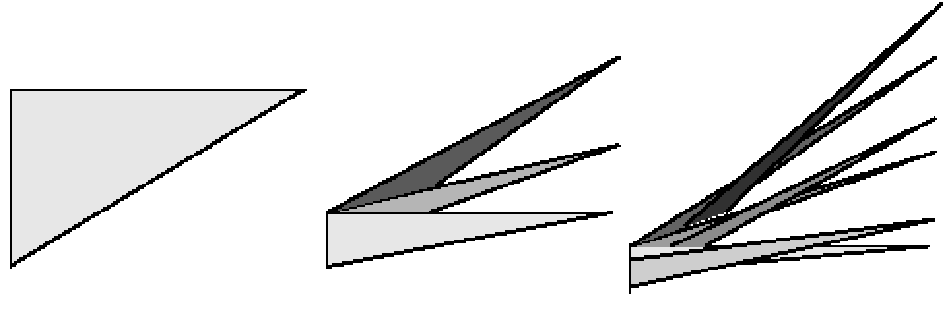
(de nombreuses autres constructions ont été proposées).

Encore plus surprenant, en 1965, Cunningham et Schönberg on prouvé que si l'on imposait à la figure décrite par l'aiguille d'être convexe, il n'y avait toujours pas d'aire minimale strictement positive (quoi qu'aient pu en affirmer certains auteurs par la suite).