Le paradoxe des anniversaires
Sémantique
Logique
Infini
Mesure
Probas
Nombres
Physique
C'est un domaine fourni en pseudoparadoxes : résultats rigoureux, mais choquant l'intuition car le bons sens, particulièrement peu fiable, aurait volontiers donné une réponse différente.
Un exemple simple pour commencer :
Combien de personnes faut-il réunir pour que la probabilité que deux d'entre elles aient le même jour anniversaire (mais pas nécessairement la même année ! D'autre part, on pourra négliger les années bissextiles, séculaires, quadriséculaires...) soit supérieure à 1/2 ?Le naïf observera qu'avec 366 personnes ne réunion, il est certain que deux soient nées le même jour. Il répondra donc sans réfléchir, comme il se doit : 366/2 = 183 ! C'est assez éloigné de la bonne réponse, comme nous allons le voir.
Cherchons plutôt la probabilité Pn pour que n personnes n'aient aucun anniversaire en commun. Bien sûr, P1 = 1 = 365/365. Avec deux personnes, la seconde peut être née n'importe lequel des 364 jours autres que l'anniversaire de la première. Donc P2 = 365/365 × 364/365. Avec trois personnes, la troisième n'a plus le choix qu'entre 363 jours, donc : P3 = 365/365 × 364/365 × 363/365. On voit facilement se dessiner une formule générale :
| Pn | = |
|
|||||||||||
| = |
|
||||||||||||
| = |
|
Le problème initial revient alors à résoudre Qn = 1−Pn > 1/2 soit Pn < 1/2. Une calculatrice très simple (même Maple) suffit alors pour faire la calcul :
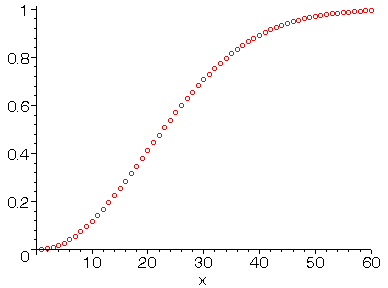
En prime Maple nous fait un beau dessin pour montrer l'évolution de Qn en fonction de n (Q60 est déjà ≃ 0,994 ; il est inutile de tracer au-delà).